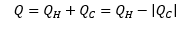Sin embargo, existe otro principio, independiente de la primera ley y que no se deduce de ella, el cual determina la fracción máxima de calor que un motor puede convertir en trabajo mecánico. El fundamento de este principio radica en la diferencia entre la naturaleza de la energía interna y la energía mecánica. Microscopicamente sabemos que la energía interna se refiere al movimiento molecular aleatorio, mientras que la energía mecánica se refiere al movimiento ordenado de las moléculas. Superpuesto a su movimiento aleatorio, las moléculas de un cuerpo tienen un movimiento ordenado en la dirección de la velocidad del cuerpo, este movimiento es el que conocemos como energía cinética, es decir, la energía cinética asociada al movimiento ordenado de las moléculas. La energía cinética y potencial asociada con el movimiento aleatorio constituye la energía interna. Cuando un cuerpo choca inelásticamente, según la primera ley de la termodinámica se genera calor, de modo que la energía se conserve, este calor es producto del ahora movimiento aleatorio de las moléculas, debido a que no podemos controlar el movimiento individual de las moléculas, no es posible reconvertir por completo el movimiento aleatorio en movimiento ordenado. No obstante, podemos convertir una fracción de este en movimiento ordenado, esto es lo que hace un motor térmico.
Aunque nos hemos remitido a una explicación microscópica, tanto como la segunda ley como todos los principios termodinámicos, tratan de cantidades completamente mensurables. Esta imposibilidad de convertir completamente calor en energía mecánica constituye el fundamento de uno de los enunciados de la segunda ley.
Es imposible para cualquier sistema experimentar un proceso en el que absorba calor de un foco a una sola temperatura y lo convierta completamente en trabajo mecánico, finalizando en el mismo estado en el que empezó.
(Ningún motor térmico puede tener una eficiencia del 100%)
En el caso de no ser cierta esta ley, un barco de vapor podría navegar con tan sólo el calor del agua del mar, o el calor del aire. Se debe advertir que ninguno de estos casos viola la primera ley, pues tanto como el océano como el aire constituyen grandes depósitos de energía interna, que en principio puede extraerse en forma de calor. La primera ley niega la posibilidad de crear o destruir energía, la segunda excluye la oportunidad de utilizar la energía de un modo de determinado.
Procesos reversibles e irreversibles.
Primero consideremos un sistema en equilibrio termodinámico. Como ya lo hemos definido se trata de un sistema donde hay equilibrio mecánico, químico y térmico, donde no hay cambios de estado y se puede definir en función de variables donde no este involucrado el tiempo, estas son variables termodinámicas. Supongamos ahora que perturbamos el sistema, con esto rompemos el equilibrio termodinámico ya sea alterando la estructura interna de este, o generando alguna diferencia térmica, o variando por ejemplo su volumen; imaginemos que reducimos el volumen de un sistema mediante un émbolo. El sistema no estará en equilibrio termodinámico, pues habrá un movimiento relativo de sus partes debido a las fuerzas desequilibradas, con esta reducción del volumen puede haber un aumento de temperatura, puede haber cambios químicos o cambios de fase. Por supuesto, después de un intervalo de tiempo, si se abandona a sí mismo el sistema puede alcanzar un nuevo equilibrio termodinámico, sin embargo durante el proceso de cambio no hay este equilibrio.
Con esto el lector ya debe haber deducido que la mayoría de los procesos termodinámicos comienzan por el equilibrio, luego pasan por estados de no equilibrio, y terminan en otro estado de equilibrio. La termodinámica trata de comprender estos procesos, y esto lo hace comparando su comportamiento con el del un proceso ideal llamado proceso reversible; este consiste en cambiar el estado de un sistema mediante una sucesión ininterrumpida de estados de equilibrio.
En un sistema donde variamos el volumen, para lograr acercarse a un proceso reversible se deben efectuar cambios del volumen muy pequeños, de modo que durante todo el proceso el sistema se encuentre en un estado que no difiera mucho del equilibrio. Es decir, si empujamos ligeramente un pistón el volumen del sistema se reducirá un poco, habrá un leve cambio, pero brevemente habrá un nuevo estado de equilibrio. Aplicando sucesivamente este paso se lograra un proceso ideal en el que el sistema pasa por sucesivos estados de equilibrio. En la práctica podemos acercarnos a un proceso reversible cambiando las condiciones externas del sistema con gran lentitud.
En un proceso isotérmico, al ser la temperatura constante, se considera un proceso reversible, pues la temperatura de un sistema en conjunto tiene un valor definido sólo en un estado de equilibrio, de modo que un proceso isotermo debe efectuarse sólo en estados de equilibrio. En un proceso adiabático, al no haber flujo calorífico hacia el sistema desde el ambiente, puede ser reversible o irreversible. En la práctica no podemos obtener un aislador perfecto, de modo que un proceso adiabático se debe llevar a a cabo con mucha rapidez para que no salga o entre calor al sistema, pero en un proceso reversible el proceso se debe llevar lentamente para se alcance algún equilibrio. Sin embargo, es posible lograr que un proceso adiabático sea reversible, considerando que el tiempo que se requiere para que la presión se iguale o para que otros procesos lleguen al equilibrio es menor que el flujo de calor.
El hecho de que el trabajo pueda disiparse completamente en calor y el calor no pueda hacerlo en trabajo, expresa una unilateralidad de la Naturaleza: el calor siempre fluye del cuerpo más caliente al más frío, los gases tienden a moverse de presiones altas a bajas, la sal se disuelve en agua, pero una disolución salina no tiende a descomponerse en sal pura y en agua pura, el hierro se oxida y la gente envejece. Todos estos ejemplos se refieren a procesos irreversibles, estos es, procesos de desequilibrios.
El análisis de frigoríficos constituye otro enunciado para la segunda ley. El flujo calorífico siempre se hace del más caliente al más frío, nunca al revés. Un frigorífico lleva calor de un cuerpo frío a un foco caliente, pero su funcionamiento está determinado por el trabajo suministrado.
Es imposible para cualquier proceso tener como único resultado la transferencia de calor desde un cuerpo frío a uno caliente.
El flujo calorífico es un proceso irreversible, es decir, nunca podrá ir en dirección inversa, de igual forma la conversión de energía mecánica en calor. El segundo principio termodinámico es una expresión del aspecto unidireccional inherente de los procesos de la Naturaleza y de las limitaciones que esto impone a los motores térmicos.
El ciclo de Carnot.
A partir de la segunda ley de la termodinámica, sabemos que una máquina no puede tener un rendimiento del 100%, entonces, ¿cuál es la máxima eficiencia de un motor? Esta misma pregunta fue hecha por Sadi Carnot en 1824. Ideó un motor térmico hipotético para dar respuesta a la pregunta. Este motor tiene la mayor eficiencia posible coherente con la segunda ley, su nombre es motor de Carnot y su ciclo, ciclo de Carnot. Este ciclo consiste en una serie de procesos que regresan un sistema a sus condiciones originales. Para comprender esto tenemos que remitirnos al concepto de reversibilidad. El flujo calorífico que tiene lugar en un descenso de temperatura y la conversión de trabajo en calor son procesos irreversibles, por consiguiente, para conseguir el máximo rendimiento en un motor térmico se deben evitar todos los procesos irreversibles. De modo que durante la transferencia de calor no debe haber diferencia de temperatura finita, cuando el motor absorbe del foco caliente calor, el propio motor debe estar a esa temperatura, de otra forma se produciría un flujo de calor irreversible. De igual forma cuando se cede calor al foco frío, el motor debe estar a esa temperatura, en otras palabras, todo proceso que implique transferencia de calor debe de ser isotérmo. Todo proceso de nuestro ciclo ideal debe de ser isotermo o adiabático.
Este ciclo consiste en una sola sustancia que trabaja homogénea, tal como un gas, y está constituido por dos procesos isotérmicos y dos adiabáticos reversibles. Ahora, supongamos un cilindro provisto de un pistón, dentro del cilindro se encuentra un gas ideal. Dispondremos de dos bases conductoras, una temperatura T1 y la otra a T2, siendo T1 mayor que T2. También dispondremos de dos bases no conductoras. Consta de 4 etapas:
1. El gas se encuentra en una condición inicial P1,V1,T1. El cilindro se pone en el depósito de calor a una temperatura T1, y se deja que el gas se dilate lentamente hasta P2,V2,T2. En el proceso el gas absorbe una cantidad de calor Q1 por conducción a través de la base. El proceso es isotérmico, el gas hace trabajo levantando el pistón.
2. Se pone el cilindro en una base no conductora. Este se dilata lentamente hasta P3,V3,T3. El proceso es adiabático. El gas hace trabajo empujando al pistón.
3. Se pone el cilindro en contacto con el depósito más frío, T2. El gas se comprime lentamente hasta P4,V4,T4. En el proceso se pasa una cantidad de calor Q2 al depósito por conducción a través de la base. El proceso es isotérmico, el pistón realiza trabajo comprimiendo el gas.
4. Se pone el cilindro sobre una base no conductora. El gas se comprime lentamente hasta su posición inicial, P1,V1.T1. El proceso es adiabático. Se realiza trabajo sobre el gas.
De este modo tenemos que la variación de energía durante el ciclo es cero, pues los estados inicial y final son los mismos. A partir de la primera ley de la termodinámica tenemos:
Definimos el rendimiento o eficiencia de un máquina térmica como la relación del trabajo neto hecho por ella durante un ciclo y la cantidad de calor tomada de la fuente de elevada temperatura. Para el motor de Carnot se tiene:
Ningún motor operando entre dos temperaturas dadas puede ser más eficiente que un motor de Carnot operando entre las mismas temperaturas.
Todos los motores de Carnot operando entre dos temperaturas dadas tienen el mismo rendimiento, independientemente de la naturaleza de la sustancia.
Estos constituyen enunciados equivalentes a la segunda ley.
La última ecuación reúne las condiciones que ha de tener un motor real, para aproximarse a la eficiencia máxima. Estas condiciones son que la temperatura de entrada, T1, sea lo más alta posible y la de salida, T2, lo más baja posible. Además la temperatura de escape no puede ser menor que la más baja disponible para refrigerar la salida. Generalmente es la temperatura del aire o la del agua de un río si la planta dispone de esta. Debido a que la presión de vapor del agua aumenta rápidamente con la temperatura, el límite es impuesto por la resistencia mecánica de la caldera. A 500 grados centígrados, la presión de vapor del agua es de 235 atm, ésta es aproximadamente la presión práctica máxima de las calderas de vapor actuales.
La inevitable pérdida de calor de las centrales de energía eléctrica crea un serio problema ambiental; frecuentemente cuando se utiliza un río para refrigerar, la temperatura del agua puede elevarse a varios grados, y es esta modificación de la temperatura la que causa problemas ambientales; se le llama contaminación térmica, y es una consecuencia inevitable de la segunda ley de la termodinámica.