Estudiaremos la expansión de los gases, formulando suposiciones aisladas distintas: (1) presión constante y temperatura variante, (2) volumen constante y presión variante con la temperatura.
(1) puede ser analizado a partir de una masa gaseosa encerrada en un cilindro provisto de un pistón móvil. La presión P1 se considerará constante, y el volumen V1 es el volumen del gas a una temperatura 0℃ y Vt el volumen del gas a una temperatura t. Al aumentar la temperatura, el volumen del gas aumentará linealmente con la temperatura. Los datos experimentales se expresan por la ecuación:
donde β es una constante, la cual podemos definir como:
Se deduce que β es el coeficiente de dilatación cúbica de un gas a presión constante, la cual es proporcional a la pendiente de una gráfica de Volumen- Temperatura. El hecho notable aquí es que β es prácticamente constante e igual a 1/273=0,0366 por grado centígrado para todo los gases permanentes ( entendemos como gases permanentes como aquellos gases que no pueden licuarse solo con presión a temperaturas normales): hidrógeno, oxígeno, helio, neón, nitrógeno...
Para (2) disponemos de un gas encerrado en un recipiente de volumen constante y variamos la temperatura. Se encuentra entonces que la presión de un gas (P), aumenta con la temperatura de acuerdo con la ecuación:
donde P1 es la presión inicial a una temperatura de 0℃ y Pt es la presión a una temperatura t. La constante γ se llama coeficiente de variación de presión a volumen constante. Se encuentra experimentalmente que β es aproximadamente igual a γ (1/273), todo esto para los gases permanentes.
Como β=γ=1/273, tenemos reemplazando en la ecuaciones anteriores
donde V1 es el volumen a 0℃ y Δt es el cambio de temperatura. Si la temperatura baja de 0℃, por ejemplo para la primera ecuación, el volumen disminuye en 1/273 de su valor a 0℃. Obviamente, a -273 ℃ disminuirá todo su valor inicial a 0, a temperaturas aun menores, tendrá un volumen negativo, lo cual no tendría sentido físico. En efecto, -273℃ es un cero absoluto y no puede existir gases a temperaturas menores. Lord Kelvin propuso una nueva escala de temperaturas, la cual hoy día lleva su nombre, grados Kelvin o Temperatura Absoluta. En esta escala 0°C=273°K (T=t°C+273). Haciendo uso de esta escala, las ecuaciones se reducen a
La primera sucede a volumen constante y la otra a presión constante. La segunda ecuación es la expresión analítica de la ley de Charles, la cual dice: "a presión constante el volumen de una dada masa gaseosa varía en proporción directa con la temperatura absoluta".
Ahora, para la resolución de problemas, las ecuaciones anteriores pueden escribirse
Si una dada masa de gas a una temperatura T1 tiene un volumen V1 y se calienta a la temperatura T2, adquirirá un volumen V2. De igual forma la presión, si se tiene una masa gaseosa a una presión P1 y a una temperatura T1, encerrado en un volumen constante, y si luego se calienta a una temperatura T2, tendrá entonces una presión P2. La primera ecuación sucede a volumen constante y la segunda a presión constante.
Una pregunta que se puede estar haciendo el lector en este momento es, ¿y que pasa si la temperatura es constante y comprimimos un gas mediante un pistón? es decir, ¿que pasa si solo variamos la presión y el volumen de un gas? La respuesta viene de dada por ley de Boyle la cual dice: " el producto de la presión por el volumen de una dada masa gaseosa es constante a temperatura constante"
donde el valor numérico de C depende de la temperatura a la que este sometido el gas. Los gases que cumplen las ecuaciones anteriores son por definición gases ideales; los gases como el hidrógeno, helio, oxígeno, nitrógeno, etc, pueden considerarse como gases ideales, esta aproximación aumenta a presiones bajas y temperaturas altas. También hay que decir que la ecuación de Boyle es aplicable sólo a gases en Estado De Equilibrio; y por Estado De Equilibrio entendemos que cuando un gas se halla a una temperatura constante T, si ocupa un volumen definido V, y si se halla sometido a una presión externa constante P, este gas no tendrá ninguna tendencia a cambiar su estado. Un caso en la que la ecuación no puede utilizarse es cuando el gas se expande rápidamente.
De igual manera que las otras ecuaciones, la ley de Boyle pude formularse así
 |
| (temperatura constante) |
Ecuación de estado de los gases
Ahora, ¿que pasa si la presión, el volumen y la temperatura varían? esta ecuación que describe el comportamiento de un gas cuando P,V y T varían simultáneamente se halla combinando las ecuaciones que de Charles y Boyle, así
R es la constante del gas, y depende de la naturaleza y de la masa del gas. Podemos escribir convenientemente la ecuación así
Además, si tomamos en cuenta si una dada masa M1 ocupa un volumen V1 a una presión P1 y a una temperatura T1 y si una masa M2 del mismo gas ocupa un volumen V2 a una presión P2 y a una temperatura T2, puede demostrarse que
y tomando en cuanta que densidad ρ es igual a masa sobre volumen, tenemos
Calentamiento de un gas durante una comprensión.
Se sabe experimentalmente que si se comprime un gas en un cilindro, el gas se calienta , pues cuando un gas se comprime se realiza trabajo sobre el gas, y según el primer principio de la Termodinámica se genera calor; en el caso de que el gas se expanda, el gas realiza trabajo sobre el pistón, al hacerlo mover contra la presión atmosférica, y por tanto el gas se enfría. La ley de Boyle, frente a estos hechos, es aplicable siempre y cuando las expansiones y comprensiones se sucedan lentamente, de tal manera, que el gas tenga tiempo de adaptarse a sí mismo y mantener constante su temperatura.





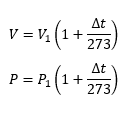







No hay comentarios:
Publicar un comentario